 |
||
|
Формы представления параметров запаздывающих нейтронов М.Н.Зизин, НИЦ КИ, г. Москва, ОПУБЛИКОВАНО 09.11.2014
К счастью, не о всём ещё подумано. Станислав Ежи Лец Введение Одной из целей реакторного сообщества в ближайшем будущем является создание системы тестов, которую можно было бы использовать при разработке следующего поколения программного обеспечения. В этой связи следует отметить, что тестов для решения нестационарных нейтронно-физических задач немного и пришло время задуматься о пополнении этого семейства. Основной и самый простой способ - это включение в уже имеющиеся "стационарные" тесты формулировок для пространственно-временного расчёта с описанием требуемых функционалов и дополнительной входной информации по кинетическим параметрам отдельных нуклидов. Примеры такого подхода есть [1, 2], но нужна его формализация. Здесь мы рассматриваем расширение теста BN600_IAEA. По сравнению с работой [1] используются полномасштабные модели и изменено положение имитаторов ионизационных камер (по аналогии с тестовой моделью реактора БН1200 [3]). Одной из целей данной работы является привлечение внимания к тестам такого рода. С помощью этого теста исследуется влияние форм представления параметров запаздывающих нейтронов (ЗН) на значения эффективности стержней аварийной защиты при пространственно-временных расчётах. Использовалась константная система CONSYST Ver.0601 с константами БНАБ-93. 1. Описание модели теста BN600_IAEA. Входные данные для теста BN600_IAEA (название теста условное) были подготовлены OKBM и ФЭИ (Россия) для МАГАТЭ в рамках проекта "Обновлённые коды и методы, предназначенные для уменьшения вычислительной неопределённости эффектов реактивности в быстрых реакторах с натриевым теплоносителем (LMFR)" [4]. Итоговые отчёты опубликованы в 2010 и 2013 гг. и доступны в интернете [5]. Вот описание модели, данное Серёгиным А.С. (частное сообщение). При подготовке тестовой модели BN600_IAEA были приняты следующие упрощения фактической картограммы активной зоны: - границы зон обогащения симметризованы по азимуту; - стальной боковой экран переменной по азимуту толщины преобразован в экран с одинаковой усреднённой толщиной; - исключено внутриреакторное хранилище с его защитой из карбида бора; - два регулирующих стержня РС заменены на ТВС зоны малого обогащения ЗМО, а два близлежащих компенсирующих стержня КС переставлены по направлению к центру активной зоны в ячейки, симметричные остальным четырём КС внутреннего кольца; - исключены две ячейки с фотонейтронными источниками. На периферии тестовая модель ограничена стальным экраном (сборками стальной защиты), за которым задан один ряд сборок стального отражателя. Для сохранения эффективного коэффициента размножения и распределения мощности по основным зонам реактора как в проектной модели, несколько увеличено погружение компенсирующих стержней в активную зону. Модель соответствует состоянию работы на номинальной мощности в начале стационарного цикла, когда существенно влияние системы поглощающих стержней. Модель представляет ценность для проверки программ, реализующих расчёт нейтронно-физических характеристик быстрых реакторов вместе с расчётом сечений, так как имеется достаточно большая база для сравнений. На периферии расчётная модель ограничена радиальной защитой (стальные сборки), следующей за одним рядом сборок радиального отражателя. Граничные условия соответствуют равенству нулю потока на границе реактора (φ=0). Расчёты эффективности аварийной защиты (АЗ) в начальную постановку тестовой задачи BN600_IAEA не входили. В работе [1] в 60° симметрии моделировался пространственно-временной процесс после мгновенного сброса всех стержней АЗ (Scram Rods), где реактивность оценивалась на основе обращённого решения уравнения кинетики (ОРУК) с подстановкой в него как локальных, так и интегральных функционалов. Расчёты проводились в гексагональной и треугольной 3D-геометрии для модели с 60° симметрией. В качестве локальных функционалов, имитирующих токи ионизационных камер, использовались потоки нейтронов на внешней границе реактора в центральной плоскости. После появления тестовой модели реактора БН-1200 [3], где четыре ионизационные камеры (ИК) расположены на верхней границе активной зоны, я решил разместить имитаторы ИК в модели BN600_IAEA аналогичным образом (см. Рис.2-3). Рис.1. Картограмма тестовой модели BN600_IAEA  Рис.2. 2D-модель BN600_IAEA в гексагональной (HEX) геометрии с четырьмя имитаторами ИК  Рис.3. 2D-модель BN600_IAEA в треугольной (TR) геометрии с четырьмя имитаторами ИК 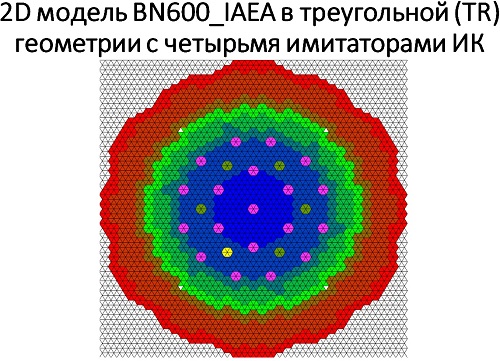 Кроме того, целесообразно моделировать падение всей щётки стержней АЗ (Scram Rods, седьмой тип - SCR7) с застреванием одного из стержней, подобно тому, как это делается в реакторах ВВЭР-1000 [7], а также падение одиночного стержня АЗ. Этот стержень Scram Rod (SCR11) на Рис.2 и 3 выделен жёлтым цветом. Несимметричность картограммы с выделенным стержнем SCR11 вынуждает проводить расчёты 360° полномасштабной модели. Расчёты проводились с 63 точками по высоте реактора как в треугольной, так и в гексагональной модели, при скорости падения стержней SCR 1 м/с. Расчёты гексагональной модели с 21 точкой по Z дают неприемлемые результаты. Нодальные методики не использовались. Гексагональная модель при использовании обычных конечно-разностных методов с одной точкой на гексагон рекомендуется для отладочных расчётов, поскольку эффективность АЗ существенно отличается для HEX и TR геометрий. Tаблица 1. Составы и размеры ячеек по высоте. Сверху вниз - с 63 точками по Z. 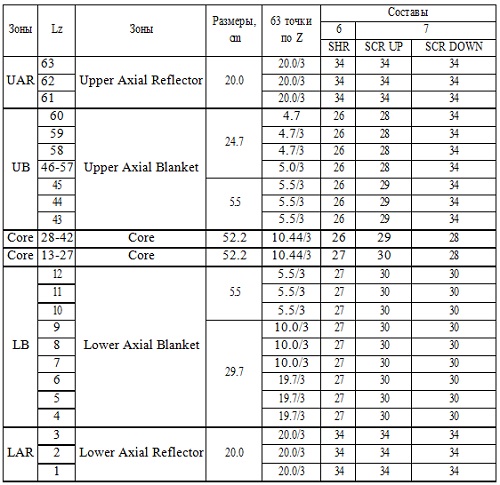 Составы зон и их распределение по высоте реактора можно найти в [1, с.116]. 2. Основные нестационарные уравнения переноса нейтронов. Запишем групповое нестационарное диффузионное уравнение переноса нейтронов в групповом приближении в форме, включающей в себя параметры ЗН. 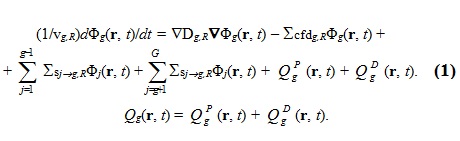 Стационарное диффузионное уравнение для ценности нейтронов: 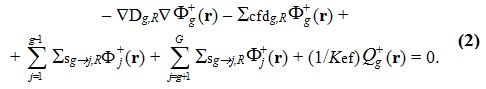 Здесь:
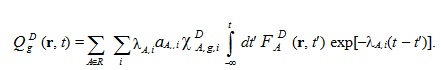 Интегральная форма источника ЗН используется в ОРУК. А при решении уравнения переноса используется дифференциальная форма: 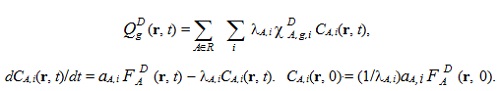 Если исключить нуклидную зависимость кинетических параметров и концентрации предшественников ЗН: 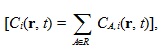 то: 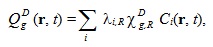 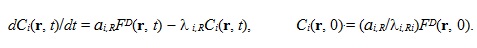 Для удобства введены дополнительные функционалы - скорости генерации мгновенных и ЗН: 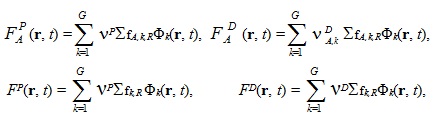 и суммарные скорости генерации нейтронов (мгновенных + запаздывающих): 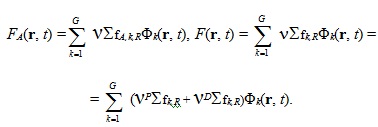 Для стационарных задач из соответствующих функционалов просто убирается зависимость от времени. Здесь и далее: Kef - наибольшее собственное число стационарной задачи, обеспечивающее её псевдокритичность за счёт ν. Индексы, их границы и параметры массивов: - A - нуклид; - D - запаздывающие нейтроны; - G - количество энергетических групп; - f - индекс при сечении деления; - i - номер группы ЗН; - j, k, g - номера энергетических групп; - P - мгновенные нейтроны; - r - координаты геометрической точки; - R - физическая зона; - t - момент времени. Зависимость сечений от времени в записи этих уравнений для простоты опущена. Макросечения размножения мгновенных нейтронов обычно отсутствуют в наборах констант, но при необходимости их можно вычислить как разность макросечений, включающих мгновенные и ЗН, и макросечений ЗН. Величины Вместо Реально в наборах данных приводятся два числа, характеризующих выход ЗН на один акт деления: 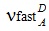 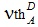 . .Для второй группы из 26 (4,0 - 6,5 МэВ) самый простой способ вычисления: 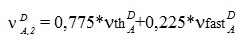 Для остальных групп: 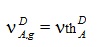 . .Граничные и начальные условия - обычные: плотность потока и ценности равны нулю на внешней границе, а плотность потока в начальный момент времени для (1) равна плотности потока из стационарной задачи. В случае, если неизвестны позонные спектры мгновенных нейтронов, то они могут быть рассчитаны как: 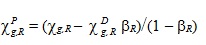 . .3. Обращённое уравнение кинетики. Появилась идея оценивать реактивность из варианта формулы ОРУК, в которой непосредственно используются концентрации предшественников ЗН Преимуществом такого подхода является тождественность приближений для учёта ЗН при решении уравнения переноса и ОРУК. Умножим (1) на Используя граничные условия на поверхности реактора, в приближении мгновенного скачка получим: 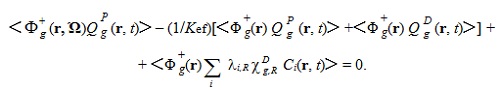 Производной по времени пренебрегаем из-за малого вклада в реактивность. В расчётах этот член ОРУК оценивался, и он действительно очень мал. Здесь символом 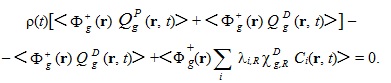 Введя: 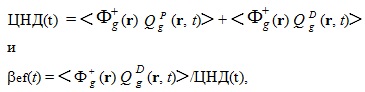 Получим: 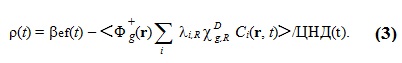 Здесь ρ(t) - реактивность, обычно трактуемая как мера отклонения от критичности в момент времени t. В принципе, если для каждого момента времени t решать возмущённую задачу (2), определяя Kef(t), то 4. Приближения при решении уравнения переноса и ОРУК при расчётах теста BN600_IAEA. В пространственно-временном уравнении диффузии в программе DDD_T_P_NO_AC источник рассчитывается как: 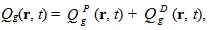 где
Традиционное обращённое уравнение кинетики для простоты выпишем тоже в приближении мгновенного скачка [7, 6, с.45]: 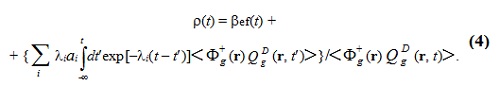 Вычисление функционалов, входящих в уравнение переноса и ОРУК, будет разным в разных приближениях. Таблица 2. Приближения при решении уравнения переноса.  Таблица 3. Приближения при вычислении реактивности ρ(t) с помощью ОРУК. 
Таблица 4. Эффективность стержней АЗ, оценённая с использованием различных приближений. 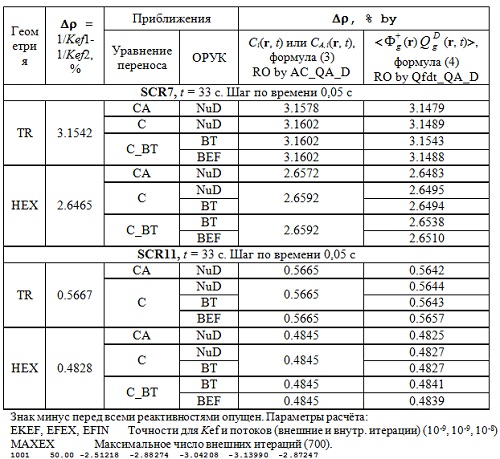 Таблица 5. Эффективность стержней АЗ, оценённая с использованием различных функционалов. 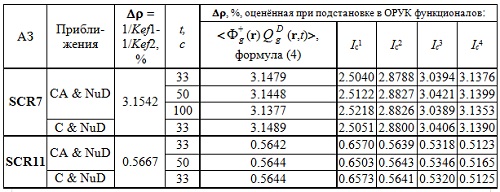 Рис.4. Эффективность стержней SCR7, оценённая с использованием различных функционалов. 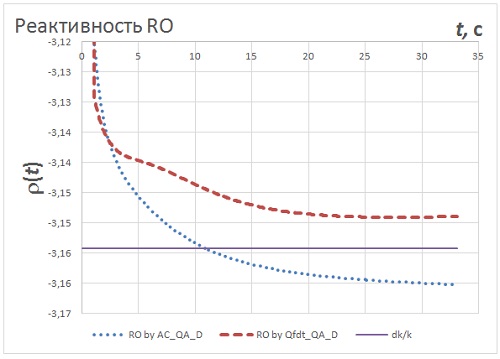 Рис.5. Эффективность стержней SCR7, оценённая с использованием различных функционалов. 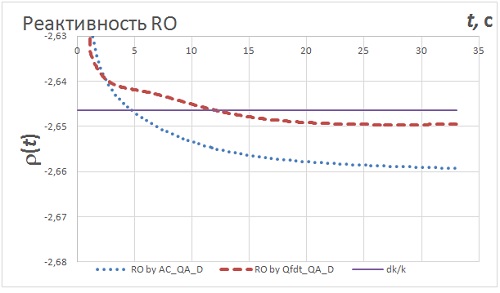 Рис.6. Эффективность стержней SCR7, оценённая с использованием различных функционалов. Гексагональная геометрия, приближения C & NuD. Шаг по времени 0,1 с. Интервал 0-35 с. 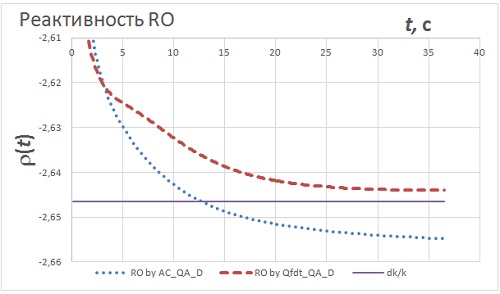 Рис.7. Эффективность стержней SCR7, оценённая с использованием различных функционалов. 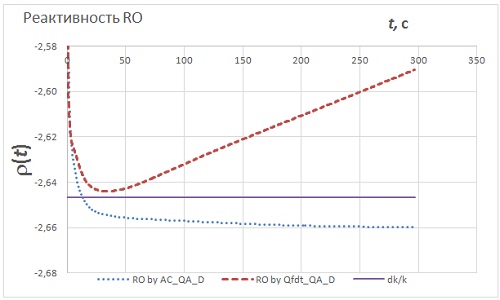 Рис.8. Эффективность стержня SCR11, оценённая с использованием различных функционалов. 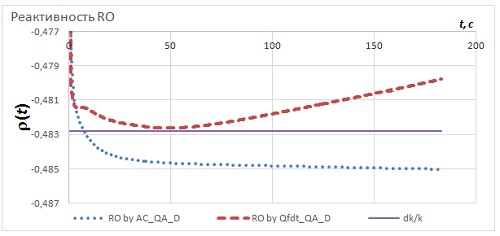 Рис.9. Эффективность стержней SCR7, оценённая с разными шагами по времени 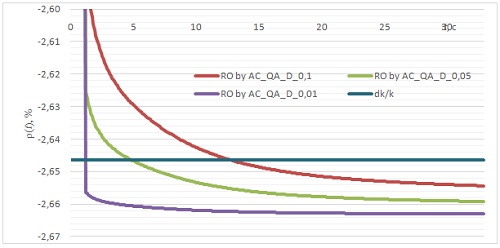 Выводы 1. Пространственно-временная тестовая модель BN600_IAEA может быть рекомендована для отладки и тестирования как собственно уравнения переноса в треугольной и гексагональной геометриях, так и для обработки полученных результатов с помощью ОРУК. 2. С практической точки зрения все использованные приближения дают разумные результаты, пригодные для обсчёта экспериментальных данных. 3. Сочетание приближений "C-NuD" и "C-BT" дают почти одинаковые результаты. 4. Переход от приближения CA к C практически не меняет результата (<0,1%), что позволяет рекомендовать отказаться от нуклидной зависимости при расчёте концентрации предшественников ЗН. 5. При расчёте эффективности одиночного стержня (|Δρ| < βef) все приближения дают меньше отличающиеся между собой результаты, чем эффективности щётки АЗ (SCR7) с застрявшим стержнем SCR11. 6. Подстановка в ОРУК потоков, имитирующих токи ИК, даёт плохие результаты. 7. Исследованная зависимость результатов от временного шага даёт разброс того же порядка, что и разные формы представления параметров ЗН. 8. Критерием выбора приемлемого шага по времени может служить время выхода на асимптотическое значение реактивности (см. Рис.9). 9. Эффекты зависимости результатов от временного шага и форм представления параметров запаздывающих нейтронов могут компенсировать друг друга. 10. Реактивности, вычисленные с помощью варианта формулы ОРУК, в которой непосредственно используются концентрации предшественников ЗН (RO by AC_QA_D), и по традиционной форме ОРУК (RO by Qfdt_QA_D), демонстрируют разные формы поведения во времени, что требует дополнительного осмысления. Список литературы [1] - Зизин М.Н. Пространственно-временной расчёт падения аварийной защиты в рамках тестовой модели BN600_IAEA. "Нейтронно-физические проблемы атомной энергетики (НЕЙТРОНИКА)". Сборник докладов ежегодных межведомственных семинаров 2009-2011 гг. Т. 1, сс. 122-131. [2] - Бояринов В.Ф., Кондрушин А.Е., Фомиченко П.А. Разработка пространственно-временного бенчмарка C5G7-TD для верификации нейтронных кодов. - В сб.: 11-я Курчатовская молодёжная научная школа, 12 - 15 ноября 2013 г., М.: с. 22. [3] - Анализ результатов расчёта нейтронно-физических характеристик реактора БН 1200 на базе тестовой модели активной зоны. Авт. С.Б. Белов и др. [1], т. 2, сc. 433-442. [4] - IAEA. Working Material: Updated Codes and Methods to Reduce the Calculational Uncertainties of the LMFR Reactivity Effects. The first Research Coordination Meeting, Vienna, 24-26 November 1999. IAEA-RC-803. IWG_FR/100 (2000). Input data for BN-600 hybrid core benchmark calculations. [5] - BN-600 Hybrid Core Benchmark Analyses. Results from a Coordinated Research Project on Updated Codes and Methods to Reduce the Calculational Uncertainties of the LMFR Reactivity Effects. IAEA-TECDOC-1623. February 2010.http://www-pub.iaea.org/MTCD/publications/PDF/te_1623_web.pdf BN-600 MOX Core Benchmark Analysis. Results from Phases 4 and 6 of a Coordinated Research Project on Updated Codes and Methods to Reduce the Calculational Uncertainties of the LMFR Reactivity Effects. IAEA-TECDOC-1700, IAEA, Vienna, 2013. http://www-pub.iaea.org/MTCD/Publications/PDF/TE-1700_web.pdf. [6] - Зизин М.Н. Методы расчёта нейтронно-физических характеристик быстрых реакторов. М.: НИЦ "Курчатовский институт", 2014. [7] - Зизин М.Н., Иванов Л.Д. О трактовке обращённого уравнения кинетики и пространственно-временных расчётов эффективности аварийной защиты ВВЭР-1000. // ВАНТ. Сер. Физика ядерных реакторов, 2012, вып. 2, c. 28-43. Ключевые слова: Нейтронно-физические расчёты реакторов, Курчатовский институт, Статьи, Михаил Зизин Другие новости: Теменужка Петкова - министр энергетики Болгарии Она представляет партию ГЕРБ. Над французскими ядерными объектами продолжаются полёты неизвестных беспилотников. Договорённости РФ о вывозе ядерного материала могут стать частью сделки Ирана и шестёрки Наши партнёры знают о такой возможности. |
Герой дня 
Валерий Коробейников: топливные циклы - это важно От России мы являемся основным поставщиком информации для экспертов, которые заняты в ИНПРО. Также мы участвуем и в постановке задач. Например, какими могут быть сценарии развития мировой атомной энергетики? ИНТЕРВЬЮ
Игорь Жемков МНЕНИЕ
МСВАЭП Последние новости:
|
© AtomInfo.Ru – электронное периодическое издание, 2006-2025.
16+, для детей старше 16 лет.
Учредитель ЭПИ AtomInfo.Ru - ООО Проект-А.
Главный редактор - Уваров А.А.
E-mail: atominfo@obninsk.ru. Телефон редакции: +7-48439-94831.
Свидетельство о регистрации СМИ Эл №ФС77-30792. Выдано Федеральной службой по надзору в сфере массовых коммуникаций,
связи и охраны культурного наследия 26 декабря 2007 года.
ATOMINFO™ - зарегистрированный товарный знак.
Использование и перепечатка материалов допускается при указании ссылки на источник.
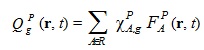 - источник мгновенных нейтронов,
- источник мгновенных нейтронов,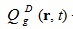 - источник ЗН, который может быть записан в интегральной или дифференциальной форме:
- источник ЗН, который может быть записан в интегральной или дифференциальной форме: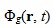 - плотность потока нейтронов;
- плотность потока нейтронов;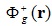 - ценность нейтронов;
- ценность нейтронов;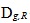 - коэффициент диффузии;
- коэффициент диффузии;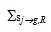 - макросечение рассеяния из группы j в группу g;
- макросечение рассеяния из группы j в группу g;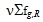 - макросечение размножения нейтронов;
- макросечение размножения нейтронов;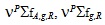 - макросечения размножения мгновенных нейтронов;
- макросечения размножения мгновенных нейтронов;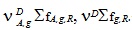 - макросечения размножения ЗН;
- макросечения размножения ЗН;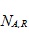 - концентрации нуклидов;
- концентрации нуклидов;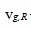 - средняя скорость нейтронов;
- средняя скорость нейтронов;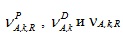 - число мгновенных и ЗН на один акт деления и их сумма, соответственно;
- число мгновенных и ЗН на один акт деления и их сумма, соответственно;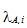 - постоянная распада предшественников ЗН;
- постоянная распада предшественников ЗН;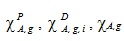 - спектры нейтронов деления - мгновенных, запаздывающих и суммарный (всегда нормируются на единицу);
- спектры нейтронов деления - мгновенных, запаздывающих и суммарный (всегда нормируются на единицу);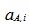 - относительный выход ЗН;
- относительный выход ЗН;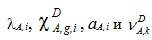 есть в наборах констант для ЗН в библиотеках БНАБ, и их можно использовать при подготовке кинетических параметров не только быстрых реакторов.
есть в наборах констант для ЗН в библиотеках БНАБ, и их можно использовать при подготовке кинетических параметров не только быстрых реакторов.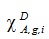 обычно используется
обычно используется 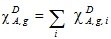 .
.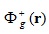 слева, (2) на
слева, (2) на 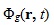 справа, проинтегрируем по объёму, просуммируем по энергетическим группам и затем вычтем одно из другого.
справа, проинтегрируем по объёму, просуммируем по энергетическим группам и затем вычтем одно из другого.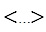 обозначено суммирование по группам g и интегрирование по пространству. К полученному выражению добавим и вычтем слагаемое
обозначено суммирование по группам g и интегрирование по пространству. К полученному выражению добавим и вычтем слагаемое 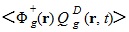 . Тогда:
. Тогда: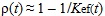 . Обычно ценность рассчитывается для конечного возмущённого состояния и для него ρ = 1 - 1/Kef.
. Обычно ценность рассчитывается для конечного возмущённого состояния и для него ρ = 1 - 1/Kef.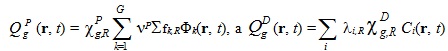 и меняется в зависимости от используемого приближения при расчёте Ci(r, t).
и меняется в зависимости от используемого приближения при расчёте Ci(r, t).
